RNA（核糖核苷酸组成的长链状分子）是基因表达中不可或缺的一环。RNA的一级结构表现为核糖核苷酸的排列，其中包含4种碱基：A（腺嘌呤）G（鸟嘌呤）C（胞嘧啶）U（尿嘧啶）。RNA的二级结构则是在一级结构的基础上，通过碱基配对产生折叠，形成多种多样的二级结构，使得RNA实现多种多样的功能。本文重点关注RNA的二级结构，并以此为背景，引入几个组合计数的问题。

一、RNA二级结构的表示：

1. 格路径表示（lattice path）：

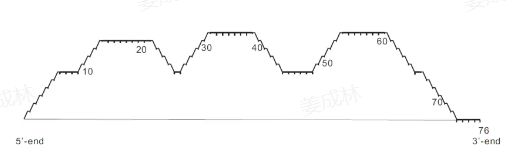
2. 山形表示：（对应格路径表示）

3. 简图表示（diagram）：

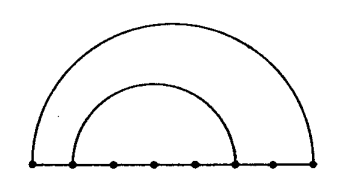
4. 圆圈表示：在简图表示的基础上，将首尾碱基对相连，形成一个圆圈。

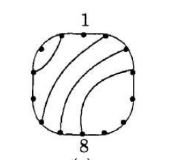
5. 文法表示（grammar）：括弧表示碱基有配对。

6. 树表示：多添加一条弧（0,32）作为根点，然后以弧作为内点，以未配对碱基作为叶子点。

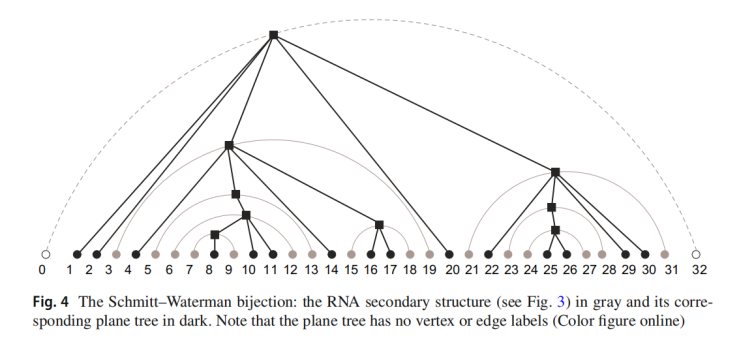
二、RNA二级结构的数学定义：

（一）$n$长的RNA二级结构可表示为一个点的标号为$[n]$的简单图，并且边集满足：

1. 若$(i,j)\in E$, 则$|i-j| \ge 2$;

2. 若$(i,j)\in E$, 且$(k,l)\in E$, 其中$i<j$, $k<l$, $[i,j]$与$[k,l]$的交集非空， 则要么$[i-j] \subset [k,l]$, 要么$[k,l] \subset [i-j]$.

（二）By Waterman: [Secondary Structure of Single-Stranded Nucleic Acids] RNA的二级结构可表示为一个含$n$“带标签”点的图，其邻接矩阵满足：

1. $a_{i,i+1}=1, 1\leq i \leq n-1.$
2. 对任意$i,\$至多存在一个整数$k \neq i-1,i+1$, 使得$a_{ik}=1$;
3. 若$a_{ij}=a_{kl}=1,i<k<l$, 则$i<l<j$.

称边$(i,k)$, $|i-k|\neq 1$为一个基对。点 $i$ 只与 $i-1$ 和 $i+1$ 相连的称为是“未配对的”。点 $i$ 被“内含于”基对$(k,l)$, 若$k<i<l$. 特别地，若不存在基对$(p,q)$, 使得$k<p<i<q$, 则称$i$是唯一内含于基对$(k,l)$的。

（三）By Tinoco et.al: [RNA Secondary Structure: A Complete Mathematical Analysis] RNA的二级结构可以表示为一个配对矩阵$P=（p_{ij}）$, 对于给定的核苷酸序列$s=s_1s_2\dots s_n$, $p_{ij}=1$当且仅当$s_i$与$s_j$配对，否则$p_{ij}=0$. 除此之外，需要满足的性质有：1. 配对矩阵的每一行每一列都至多有一个元素为1；2. 若$s_i$与$s_j$配对，则$s_k(i<k<l)$只能与$i$、$j$之间的点配对。

三、n长的RNA的二级结构的种类:

命题1. 令$R(n)$表示长为 $n$ 的RNA的二级结构的数目，则:

$R(n+1)=R(n)+\sum\limits_{j=1}^{n-1}R(j-1)R(n-j)=R(n)+\sum\limits_{j=0}^{n-2}R(j)R(n-j-1)$, 其中$n\ge2,\ R(0)=R(1)=R(2)$.

证明： 当$n=1,2$时，结果显然成立。假设对于$R(k),1\leq k\leq n$, 这一命题都成立，则对于新增的第$n+1$个碱基：

1. 它不与前$n$个碱基中的任何一个配对：此时的方案数为$R(n)$;

2. 它与前面第$j$个碱基配对：首先按照定义，第$j$个碱基不能与其余的碱基再进行配对，由于不能交叉配对，第$j+1$个碱基只能与第$j+3$个到第$n$个碱基配对。这样一来，整个RNA链被分成了两个独立的部分：$1$到$(j-1)$和$(j+1)$到$n$. 根据乘法原理，此时的方案数为：$\sum\limits_{j=1}^{n-1}R(j-1)R(n-j)·1$.

再由加法原理，相加即证毕。

易得：$R(n+1)\ge R(n)$, 所以

$R(n+1)\ge R(n)+\sum\limits_{j=0}^{n-2}R(j)R(n-1-j)=R(n)+R(n-1)+\sum\limits_{j=1}^{n-2}R(j)R(n-1-j)=R(n)+R(n-1)+\sum\limits_{j=0}^{n-3}R(j+1)R(n-j-2)\ge R(n)+R(n-1)+\sum\limits_{j=0}^{n-3}R(j)R(n-j-2)=2R(n)$

$R(n)\ge 2^{n-2}$.

更进一步地，定义生成函数:

$\phi(x)=\sum_{n=0}^{+\infty}R(n)x^{n}=1+x+\sum_{n=2}^{+\infty}R(n)x^{n}$,

则由上面所求的递推关系：

$x^2\phi^2(x)+(x-1-x^2)\phi(x)+1=0$.

命题 2. $n$长的，最小弧长为$m$的RNA二级结构的种类：

$R^m(n)=\sum_{i=1}^{m+1}R^m(n-i)+\sum_{i=0}^{n-2}R^m(i)R^m(n-2-i),n> m$

其中$R^m(0)=R^m(1)=\dots=R^m(m-1)=0,R^m(m)=1$.

证明： 当$n=1,2,\dots,m-1$时，易得$R^m(n)=1$; 假设对于$R^m(k),1\leq k\leq n-1$, 这一命题都成立，则对于新增的第$n$个碱基：

1. 它不与前$n-1$个碱基中的任何一个配对：方案数为$R^m(n-1)$;

2. 它与前面第$j$个碱基配对：首先按照定义，第$j$个碱基不能与其余的碱基再进行配对，由于不能交叉配对，第$j+1$个碱基只能与第$j+m+1$个到第$n-1$个碱基配对。这样一来，整个RNA链被分成了两个独立的部分：$1$到$(j-1)$和$(j+1)$到$n-1$.

   3. $1\leq j\leq m$: 只在$[j+1,n-1]$上形成了满足条件的二级结构，则此类二级结构数为$R^m(n-j-1)$;

   4. $m+1 \leq j\leq n-m$: 在$[j+1,n-1]$和$[1,j-1]$上都能形成满足条件的二级结构，则此类二级结构数为$R^m(n-j-1)R^m(j-1)$;

   5. $n-m+1\leq j \leq n-1$: 只在$[1,j-1]$上形成了满足条件的二级结构，则此类二级结构数为$R^m(j-1)$;

根据加法原理，总方案数为： $R^m(n)=\sum_{i=1}^{m+1}R^m(n-i)+\sum_{i=0}^{n-2}R^m(i)R^m(n-2-i),n> m$

四、RNA二级结构的各类子结构的数学定义：

1. Helix（螺旋）: RNA二级结构中的螺旋是相互嵌套的最大弧集，其左端和右端分别是连续的。这个弧集的大小称为螺旋的长度。例如$(5,13)(6,12)$就构成了一个螺旋。注意：螺旋可以只包含一条弧。

2. stack：包含基对$(p-k,q+k),(p-k+1,q+k-1),\dots,(p,q)$, 使得$(p-k-1,q+k+1), (p+1,q-1)$中至少有一个未配对。称$k+1$为stack的长度，$(p-k,q+k)$是最终的基对。

3. external vertex：不属于任何loop的未配对的点。相邻的external vertex的集合称为是external element. 若其包含点$1$或$n$, 则其为自由端（free end），否则称为joint.

4. loop（在邻接矩阵的定义下）: 若$i+1,i+2,\dots,j-1$都没被配对，而$a_{ij}=1$, 则称结构$s_{i+1}s_{i+2}\dots s_{j-1}$为loop.

5. bulge（在邻接矩阵的定义下）：若$i+1,i+2,\dots,j-1$都没被配对，而$i,j$均配对，但$a_{ij}\neq 1$, 则称结构$s_{i+1}s_{i+2}\dots s_{j-1}$为bulge.

6. interior loop：由两个bulge组成的结构$s_{i+1}s_{i+2}\dots s_{j-1}$和$s_{k+1}s_{k+2}\dots s_{l-1}, i<j<k<l$, 且$a_{il}=1,a_{jk}=1$.

7. join：特殊的bulge$s_{i}s_{i+1}\dots s_{j}$, 使得若$a_{kl}=1,k<i$, 则$l\leq i$；若$a_{kl}=1,k>j$, 则$l\ge j$.

8. tail：结构$s_1s_2\dots s_j$, 其中$1,2,\dots,j$未配对，而$j+1$配对。

9. ladder：两个序列组成的结构：$s_{i+1}s_{i+2}\dots s_{i+j}$和$s_{k+1}s_{k+2}\dots s_{k+j}, i+j+1<k,a_{i+l,k+j-l+1}=1$, 对于任何一个$1\leq l\leq j$都成立，且$a_{i,k+j+1}=a_{i+j+1,k}=0$; 若$i+j+3=k+1$, 则最后一个约束可以忽略。

10. hairpin：最长的序列$s_{i+1}s_{i+2}\dots s_{j-1}$恰好只含一个loop使得$a_{i+1,j-1}=1$, 且$a_{i,j}=0$